Overview talk (ASPDAC'25 Keynote): https://ucla.box.com/s/zu3sg20lkmlv4wwkr1ejzrbrdmjhe8lt
Related Publication:
Quantum Layout Synthesis:
- Chapter in Design Automation of Quantum Computers - Layout Synthesis for Near-Term Quantum Computing: Gap Analysis and Optimal Solution
- QCE'25 - Compilation of QCrank Encoding Algorithm for a Dynamically Programmable Qubit Array Processor
- DAC'25 - Assessing Quantum Layout Synthesis Tools via Known Optimal-SWAP Cost Benchmarks
- HPCA'25 - Reuse-Aware Compilation for Zoned Quantum Architectures Based on Neutral Atoms
- ISPD'25 - ML-QLS: Multilevel Quantum Layout Synthesis
- ASPDAC'25 - Compilation for Dynamically Field-Programmable Qubit Arrays with Efficient and Provably Near-Optimal Scheduling
- Quantum (2024) - Compiling Quantum Circuits for Dynamically Field-Programmable Neutral Atoms Array Processors
- DATE'24 (Spotlight on UCLA CQSE website) - Depth-Optimal Addressing of 2D Qubit Array with 1D Controls Based on Exact Binary Matrix Factorization
- DAC'23 - Scalable Optimal Layout Synthesis for NISQ Quantum Processors
- DAC'23 - Lightning Talk: Scaling Up Quantum Compilation – Challenges and Opportunities
- ICCAD'22 - Qubit Mapping for Reconfigurable Atom Arrays
- ICCAD'21 - Optimal Qubit Mapping with Simultaneous Gate Absorption
- IEEE Transactions on Computers (2021) - Optimality Study of Existing Quantum Computing Layout Synthesis Tools
- ICCAD'20 - Optimal Layout Synthesis for Quantum Computing
Quantum Circuit Synthesis
- ICCAD'24 - Quantum State Preparation Circuit Optimization Exploiting Don't Cares
- DATE'24 - Quantum State Preparation Using an Exact CNOT Synthesis Formulation
Architecture Optimization
- IEEE Journal on Emering and Selected Topics in Circuits and Systems (2022) - Domain-Specific Quantum Architecture Optimization
Software Release:
Benchmark:
- QUEKO: Quantum Mapping Examples with Known Optimal
- QUBIKOS - QUantum Benchamrk wIth Known Optimal SWAP Counts
Complier:
- OLSQ: Optimal Layout Synthesis for Quantum Computing
- OLSQ-DPQA: Optimal Layout Synthesizer of Quantum Circuits for Dynamically Field-Programmable Qubits Array
- OLSQ2: Scalable Optimal Layout Synthesis for NISQ Quantum Processors
- EBMF: Exact Binary Matrix Factorization
- Enola: Compilation for Dynamically Field-Programmable Qubit Arrays with Efficient and Provably Near-Optimal Scheduling
- ML-QLS: Multilevel Quantum Layout Synthesis
- ML-Sabre: Multilevel Sabre
- ZAC: Reuse-Aware Compilation for Zoned Quantum Architectures Based on Neutral Atoms
Our lab focuses on advancing quantum compilation techniques to enhance the efficiency and scalability of quantum computing. We focus on Quantum Layout Synthesis (QLS), developing optimal and heuristic methods for mapping quantum algorithms onto hardware, including reconfigurable architectures. Through benchmarking and optimality studies, we evaluate how close current techniques are to the theoretical limits. With the QLS tool, we perform architecture optimization to customize quantum hardware for improving quantum circuit performance. Lastly, we also explore Quantum Circuit Synthesis (QCS), with a focus on logic synthesis for efficient state preparation.
Outline:
Compilation in quantum computing (QC)
Quantum Layout Synthesis (QLS)
- Benchmarks - what quantum algorithm we compile?
- Optimality study - how far are we from optimal?
- Optimal quantum layout synthesis
- Multilevel quantum layout synthesis
- Layout synthesis for reconfigruable QC architectures
Quantum Circuit Synthesis (QCS)
- Logic synthesis for state preparation circuits
Architecture Optimization
Compilation in quantum computing (QC)
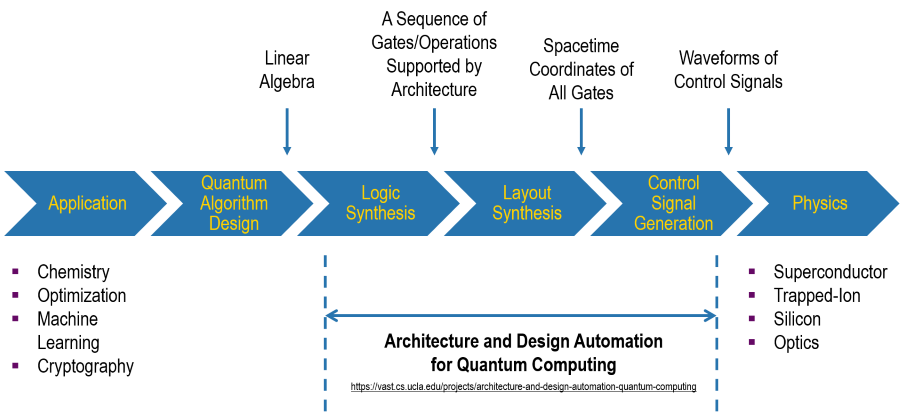
Quantum computing (QC) has been shown, in theory, to hold huge advantages over classical computing. However, there remains many engineering challenges in the implementation of real-world QC applications. In order to divide-and-conquer, we can split the task as below.
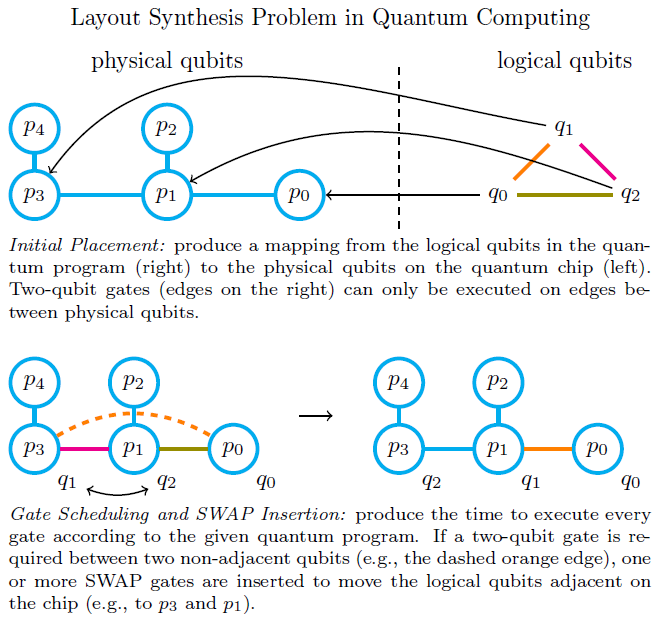
The topics that we are particularly interested in are those concerning QC architecture and compilation, which connects algorithms and devices. One of them, is layout synthesis for quantum computing (QLS), also named qubit mapping or allocation. A quantum program usually assumes all-to-all connectivity of the qubits, but this is not the case for some QC technologies. QLS aims to transform the programs so that they are executable on actual quantum hardware and, at the same time, overcome some limitations of these near-term devices, e.g. volatile qubits and error-prone quantum gates.
Quantum Layout Synthesis - QLS
Benchmarks - what quantum algorithm we compile?
The tools we have developed so far are for physical quantum circuits. If the results of these circuits are interpreted directly, the formalism of quantum computing is what we call noisy intermediate scale quantum computing (NISQ). In the long run, we may construct logical quantum circuits based on quantum error correcting codes which will translate to a huge amount of physical circuits. This formalism is called fault-tolerant quantum computing (FTQC). Introducing the middle layer of abstraction for error correction changes the compilation fundamentally. FTQC compilation is a future direction of ours while we focus on physical circuits on this page.
Our compilers are general purpose. We have used the following four benchmark sets so far.
- Arithematic circuits. These are small components for larger quantum circuits requiring arithematic manipulations. This set includes a few versions of Toffoli gate, the "NAND" for quantum computing. These circuits are results from a quantum circuit optimizer by Y. Nam, N.J. Ross, Y. Su, A.M. Childs, and D. Maslov. Automated optimization of large quantum circuits with continuous parameters. October 2017.
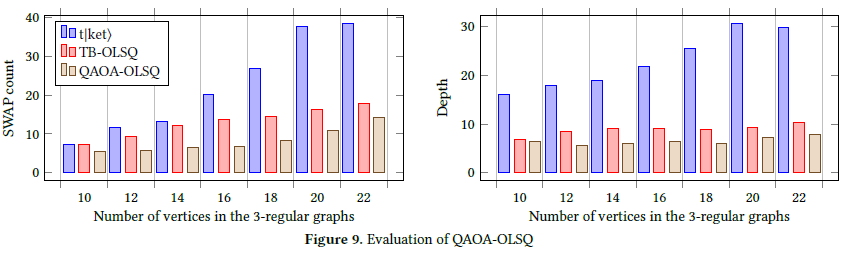
- 3-Regular MaxCut QAOA. QAOA, one of the most well-known NISQ quantum algorithms, is a quantum-classical hybrid iterative method for solving combinatorial optimization problems. An example is QAOA for the MaxCut problem where the earlist work in QAOA projects a potential quantum advantage on 3-regular graphs. We find these circuits particularly useful to benchmark compilers because 1) the graphs can be generated at quantity and with randomness, and 2) the gates are commutable, i.e., can be executed at any order, resulting in a larger solution space for the compiler.
- QUEKO as specified in the next section. This benchmark set consists of synthetic quantum circuits to measure the performance of a compiler against the theoretical optimal depth/gate count.
- QUBIKOS as specified in the next section. This benchmark set consists of synthetic quantum circuits to measure the performance of a compiler against the theoretical optimal SWAP count.
- QASMBench is a low-level, easy-to-use benchmark suite. It consolidates commonly used quantum routines and kernels from a variety of domains including chemistry, simulation, linear algebra, searching, optimization, arithmetic, machine learning, fault tolerance, cryptography, etc., trading-off between generality and usability.
Optimality study - how far are we from optimal?
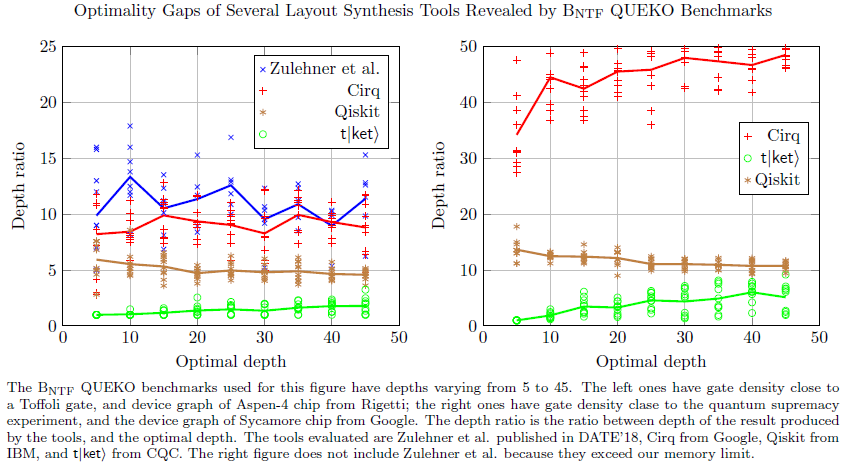
We published QUEKO, a set of QLS benchmarks with known optimal depths and gate counts on given architectures, which can be used to evaluate existing QLS tools, and direct future development of such tools. Previously, QLS benchmarks do not provide optimal solutions, so researchers can only compare with each other, but how far are they from theoretical optimum? This is an NP-hard problem to answer in general but, specifically, the optimal solutions for QUEKO benchmarks on the given architectures are known, so we can measure the optimality gaps with QUEKO. In our study, large gaps were found, even up to 45x on some near-term feasible QUEKO circuits.
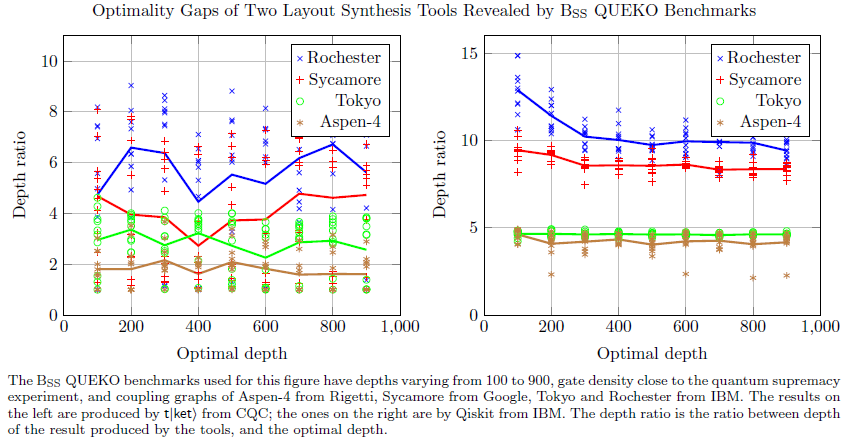
In addition to circuit depth, the number of two-qubit gates is the other important matrice to evaluate compiler performance. To this end, we propose QUBIKOS, which is the benchmark set with known-optimal SWAP count. We perform evaluation on the grid architecture (Sycamore) and heavy-hexagon architecture (Eagle). Our study shows that the performance of heuristics tools degrades with the sparse commectivity - up to 400x optimality gap even with the SOTA compiler. With the grid connecitivty, the SOTA compiler still delivers around 2x optimality gap, urging the need of high-quality compilation tool.
Optimal quantum layout synthesis
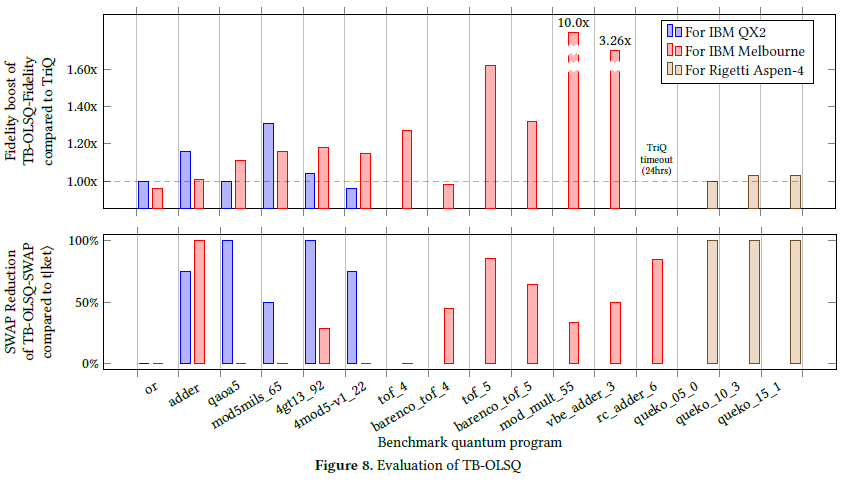
After we revealed the optimality gaps, we went on to develop an optimal/exact QLS tool, OLSQ. We represented the solution space in a more compact way, resulting in orders-of-magnitubes reductions in time and memory. By eliminating some redundant variables between mapping transformations, we arrived at a more scalable, nearly-optimal solution, transition-based (TB-) OLSQ. It can reduce 70% SWAP cost in geomean and increase fidelity by 1.3x in geomean compared to leading related works. We also applied some domain-specific knowledge to adjust TB-OLSQ in the LSQC of QAOA circuits, resulting in further reductions in depth and SWAP cost. A microgrant for open-source OLSQ has been granted by Unitary Fund.
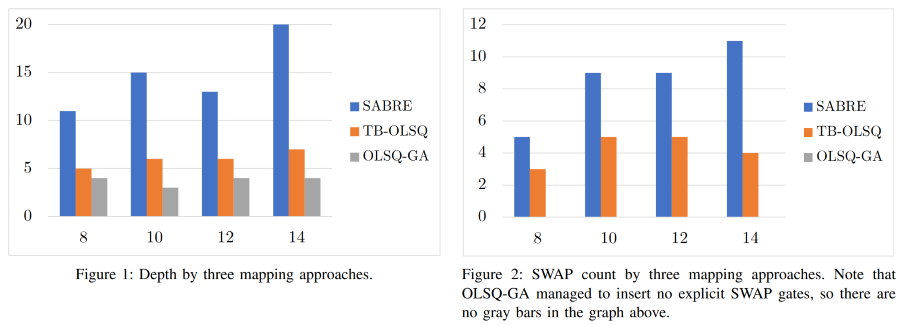
By analyzing the properties of NISQ applications, we developed three techniques improving qubit mapping quality and efficiency: SWAP absorption, commutation, and alternating matchings, which leads to OLSQ-GA, a qubit mapper that formulates the generalized NISQ mapping problem (with SWAP absorption) using SMT optimization and solves it optimally. Comparing to state-of-the-art optimal method (TB-OLSQ), we reduce depth by up to 50.0%, SWAP count by 100%. We improve fidelity by 9.45% for a single iteration, and 55.9% for 5 iterations on a set of QAOA instances. Compared to heuristic methods, the gaps are even larger.
Multilevel Quantum layout synthesis
As the rapid development of quantum hardware with 100+ qubits, optimal tools is not able to return a solution in a day due to the exponentail runtime growth. Therefore, we propse a hybrid approach multilevel quantum layout synthesis, ML-QLS, to contruct the problem hierachy by clustering. Therefore, at the coareset level, the problem size is small enough to be handled by the exact solvers. This solution will be served as the global optimization information to guide the solving process of the finer levels through the heuristic tool. As the multilevel framework is flexible in terms of the number of level, we are able to control the tradeoff between runtime and solution quality. To demoestrate that the multilevel framework can be integrated with any heuristics tools to enhance their performance, we use Sabre, which is the state-of-the-art heurisitc tool, in a multilevel scheme. Our work MultilevelSabre shows that with the aid of multilevel frameowrk, we are able to reduce SWAP count by 60% and depth by 17% depth reduction and delivers a 60% compilation time reduction.
Layout synthesis for reconfigruable QC architectures
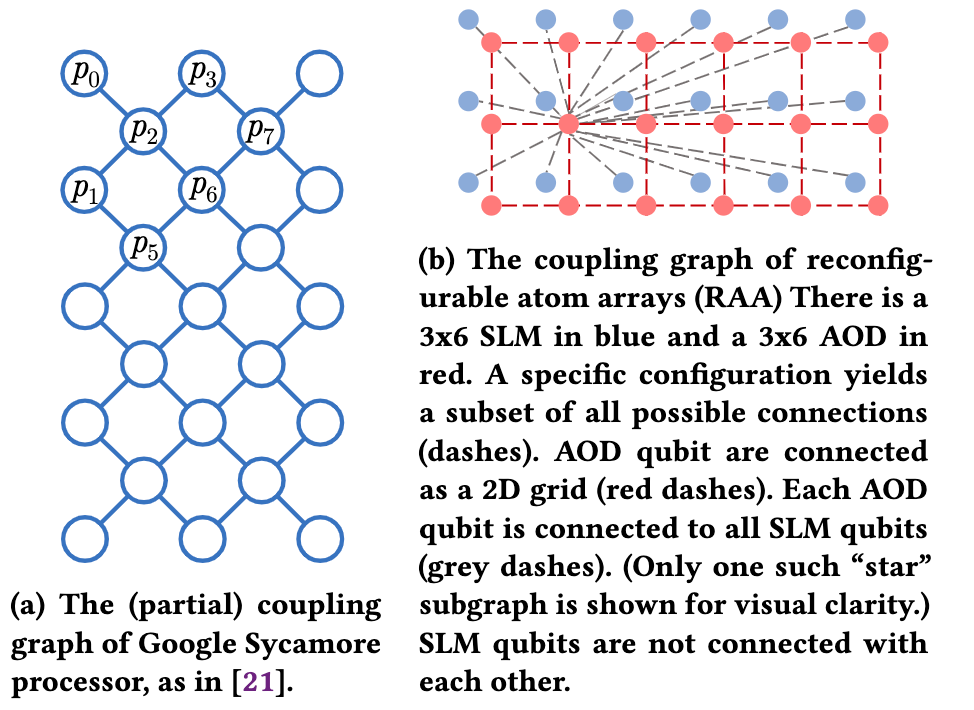
Because of the largest number of qubits available, and the massive parallel execution of entangling two-qubit gates, atom arrays is a promising platform for quantum computing. The qubits are selectively loaded into arrays of optical traps, some of which can be moved during the computation itself. By adjusting the locations of the traps and shining a specific global laser, different pairs of qubits, even those initially far away, can be entangled at different stages of the quantum program execution. In comparison, previous QC architectures only generate entanglement on a fixed set of quantum register pairs. Thus, reconfigurable atom arrays (RAA) present a new challenge for QC compilation, especially the QLS which decides the qubit placement and gate scheduling.
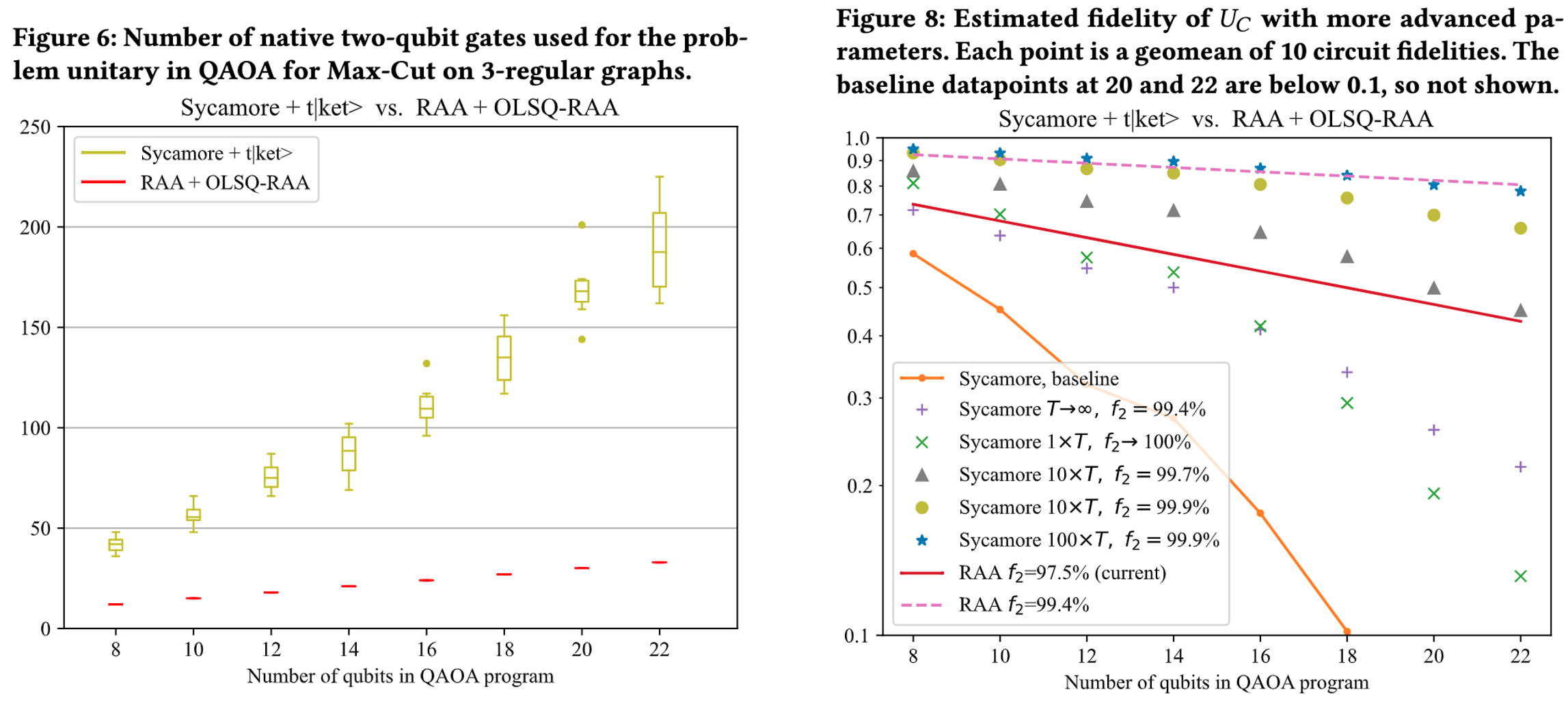
In our ICCAD'22 paper, we start by systematically examining the fundamental constraints on RAA imposed by physics. Built upon this understanding, we discretize the state space of the architecture, and we formulate layout synthesis for such an architecture to a satisfactory modulo theories (SMT) problem. Finally, we demonstrate our work by compiling the quantum approximate optimization algorithm (QAOA), one of the promising near-term quantum computing applications. Our layout synthesizer reduces the number of required native two-qubit gates in 22-qubit QAOA by 5.72x (geomean) compared to leading experiments on a superconducting architecture. Combined with a better coherence time, there is an order-of-magnitude increase in circuit fidelity.To further scale up our compiler, we learn from our previous experience in VLSI, an approach named iterative peeling. Specifically, we relax our SMT formulation so that each invocation of the solver handles as many gates as possible for one two-qubit gate stage, and the solver is called iteratively until all gates are compiled. As a result, our tool, OLSQ-DPQA, manages to compile larger circuit, e.g., the 90-qubit QAOA MaxCut shown below. This link provide a high-resolution version of the video.
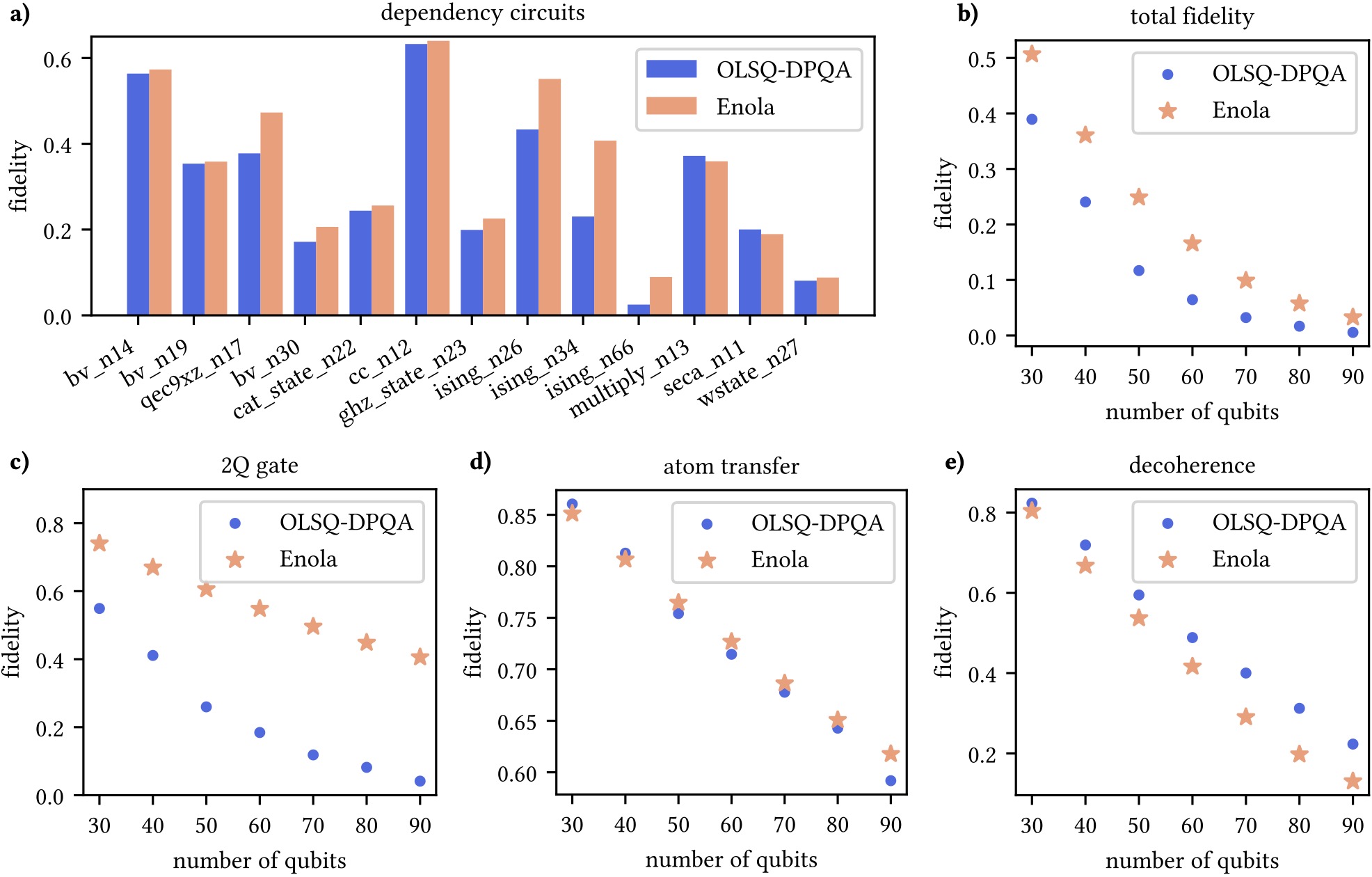
In RAA architectures, we apply a global Rydberg laser to enable two-qubit gates. However, every qubit excited by the Rydberg laser accumulates error even if they do not interact with other qubits to perform a gate. Thus, minimizing the number of Rydberg stage is critical to the circuit fidelity. In our ASPDAC'25 paper, we propose Enola with a scheduling algorithm that can achieve near optimal Rydberg laser count, and therefore achieves 5.9x fidelity improvement compared to OLSQ-DPQA.
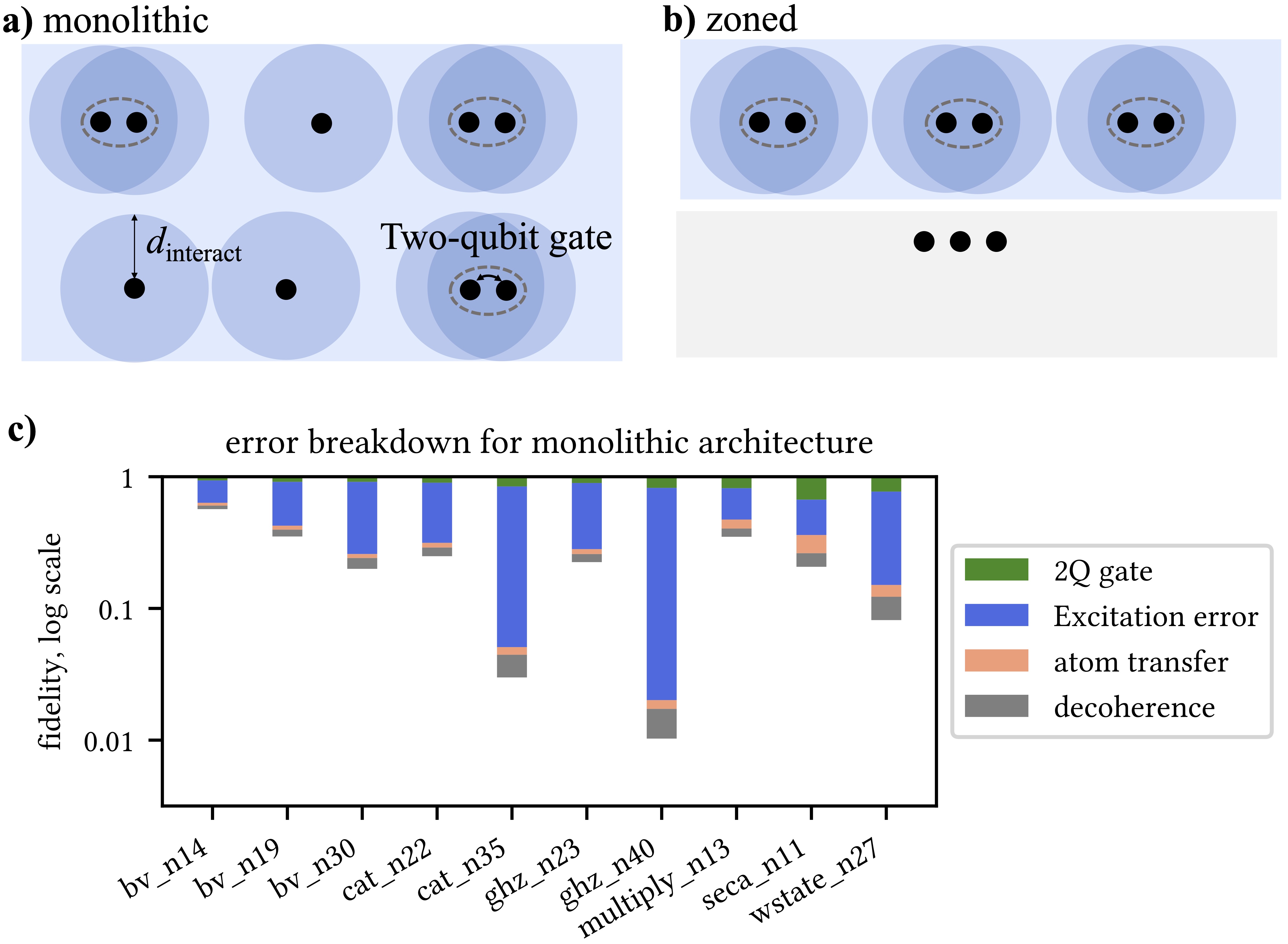
Besides the monolithic zone architectures as discussed above, zoned architectures have been proposed to mitigate the idle qubit excitation errors by having a seperate zone for qubit storage and computation. For the qubits not involved in the gate operations, they can be stored compactly in the storage zone to prevent from the effect of Rydberg laser.
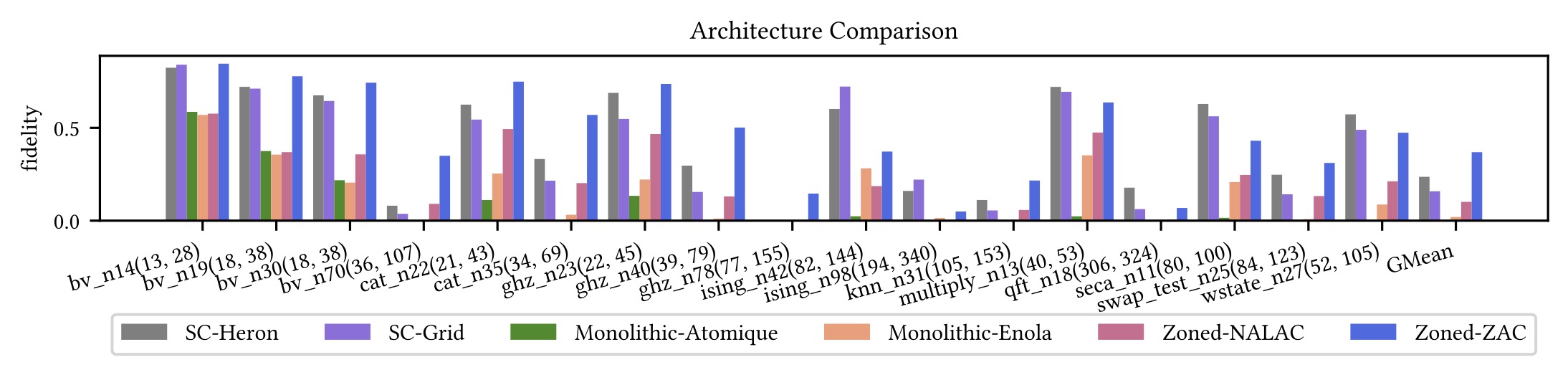
With this architecture, we would like to optimize for the qubit movement between zones as those movements will prolong the circuit execution time and thus cause qubit decoherence errors. In our HPCA'25 paper, we proposed ZAC for the zoned architecture, which significantly reduces qubit movement by the concept of qubit reuse. In addition, our qubit placement strategy effectively minimizes the qubit movement distance. Overall, we demonstrate 22x fidelity improvement over the monolithic archtecture. Moreover, ZAC is shown to only have a 10% fidelity gap on average compared to the ideal solution.
In addition, ZAC can support advanced architectures with multiple zones or AOD arrays. The animation below shows the Ising model with 98 qubits compiled for the architecture with two entanglement zone and one storage zone. The ability enables ZAC to perform architecture evalaution, facilitating the development of quantum hardware.
Quantum Circuit Synthesis - QCS
Logic synthesis for state preparation circuits
Quantum state preparation initializes the quantum registers and is essential for running quantum algorithms.
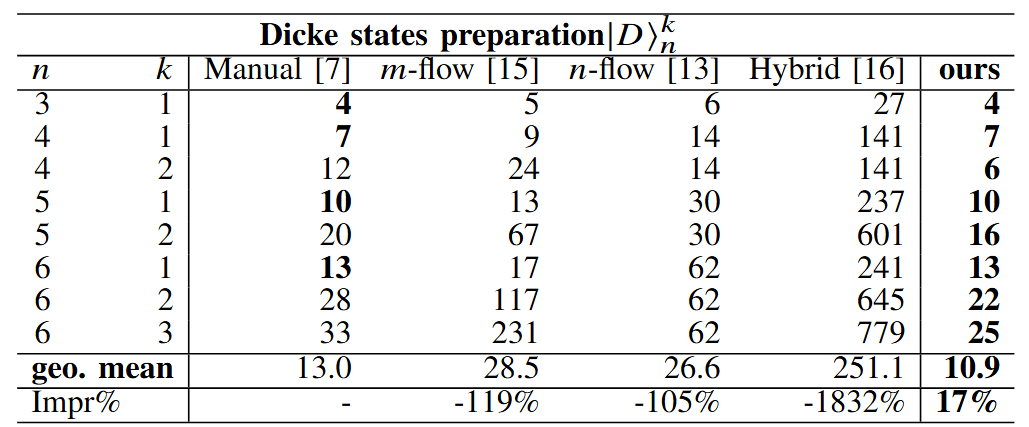
In our DATE'24 paper, we formulate the state preparation problem as a shortest path problem and employ the A* algorithm to find the circuit with optimal number of CNOTs. Our method represents a milestone as the first design automation algorithm to surpass manual design, reducing the best CNOT count to prepare a Dicke state by 2x. For general states with up to 20 qubits, our method reduces the CNOT count by 9\% and 32\% for dense and sparse states, respectively, on average, compared to the latest algorithms.
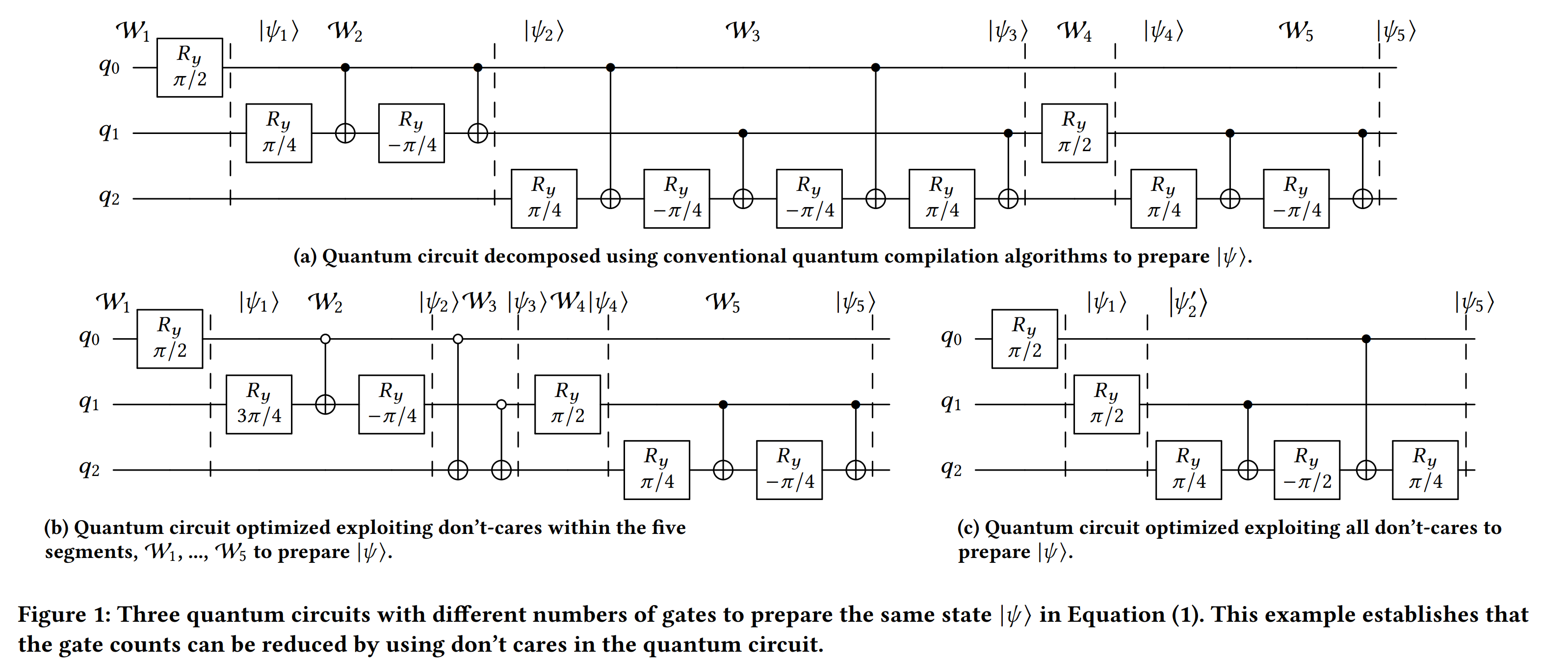
In our ICCAD'24 paper, we identify numerous conditions within the quantum circuit where breaking local unitary equivalences does not alter the overall outcome of the state preparation (i.e., don't cares). We introduce a peephole optimization algorithm that identifies such unitaries for replacement in the original circuit. Exploiting these don't care conditions, our algorithm achieves a 36% reduction in the number of two-qubit gates compared to prior methods that strictly preserves the unitary equivalency.
Architecture Optimization
Exploring architecture design with layout synthesis
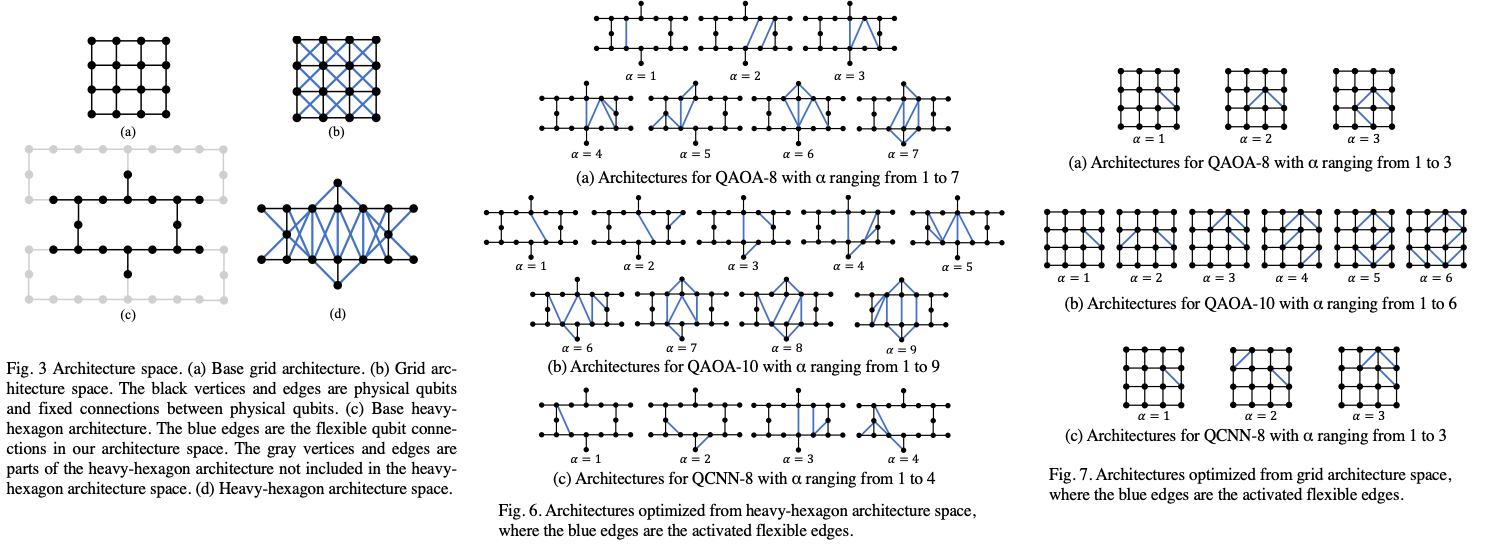
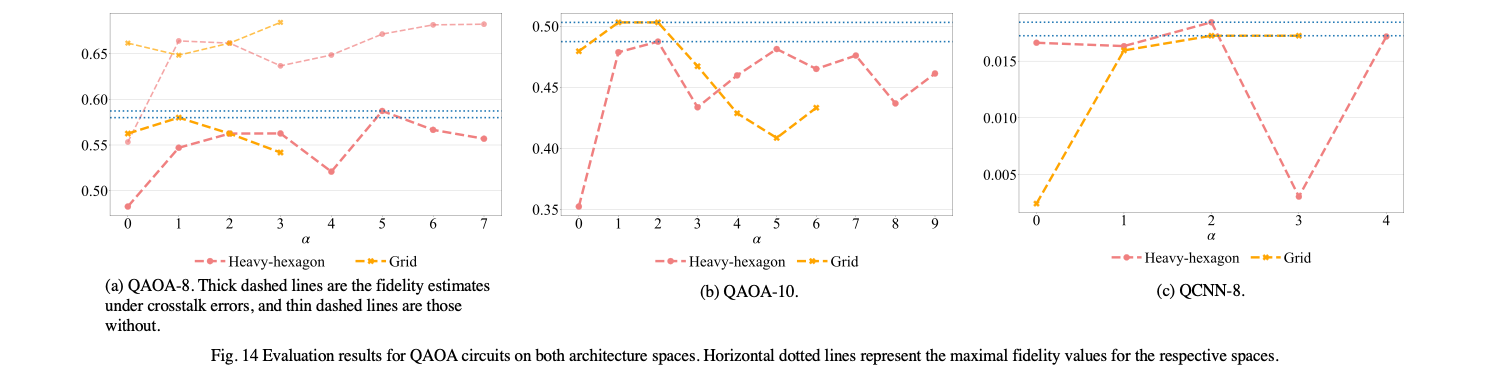
Current quantum processors are designed manually and not targeted on a specific quantum application. In classical computing, customized architectures have demonstrated significant performance and energy efficiency gains over general-purpose counterparts. For quantum computing, the qubit connectivity of quantum processors is an important factor that effects the circuit fidelity as additional computation overhead will be introduced in the QLS stage. Therefore, we focused on customizing qubit connectivity to improve fidelity for a given quantum circuit. We proposed a framework that integrates the optimal QLS tool into architecture optimization procedure in order to make the QLS tool search the architecture leading to the optimal compilation results. We demonstrate up to 59% fidelity improvement in simulation by optimizing the heavy-hexagon architecture for QAOA MAXCUT circuits, and up to 14% improvement on the grid architecture. For the QCNN circuit, architecture optimization improves fidelity by 11% on the heavy-hexagon architecture and 605% on the grid architecture.